- Is it possible to model in some detail the love dynamics between
two person by ODEs ?- Is it possible to describe a famous historic love story between two historic
persons by ODEs ?- Suppose, one person expresses its love by odes, is it possible to
express it also by ODEs ?- Is it possible to describe the poetic inspiration of a poet for writing odes by ODEs ?
All these questions can be answered positively, making use of three coupled nonlinear differential equations. Two states mimic the live for each other, coupled like a predator-prey model. A third state evaluates the poetic inspiration, depending on the love gradient.
This contribution presents in detail modelling and simulation with this model, based on mathe-matical works by S. Rinaldi and S. H. Strogatz, and on works from literary science by F. J. Jones:
- We first get to know Petrarch, a celebrated Italian poet of the 14th century, and Laura, a beautiful, but married lady, who inspires Petrarch for poems expressing ecstatic love as well as deep despair.
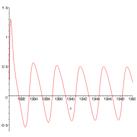
- We investigate Petrarch’s grade of poetic inspiration, established by evaluation of poems written between 1328 and 1350, showing oscillating behaviour between ecstatic love and deep despair.
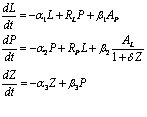
- We develop an ODE model for love dynamics of two persons, taking into account mutual attraction, rejection, and neglect
- We extend the love dynamics model by an inspiration equation, resulting from mutual feelings.
- We identify the model for Petrarch and Laura, getting an inspiration course which coincides with Petrarch’s grade of poetic inspiration, established by evaluation of the poems.
- We investigate the model analytically, and detect limit cycles, stable steady states and a bifurcation.
- We present case studies with varying parameters for attraction, rejection and neglect, using a MATLAB GUI.
- We conclude that e.g. stable steady states are good for technical processes, but not for love dynamics, and much more ……….
S. H. Strogatz: Love affairs and differential equations. Math. Magazine, 61 (1988), p. 35.
F. J. Jones: The Structure of Petrarch's Canzoniere. Brewer, Cambridge, UK, 1995.
S. Muratori and S. Rinaldi: A separation condition for the existence of limit cycles in slow-fast
systems. Appl. Math. Modelling, 15 (1991), pp. 312-318
S. Rinaldi: Laura and Petrach: an intriguing case of cyclical love dynamics.
SIAM J. App.Math.Vol. 58 (1998), No. 4, pp. 1205-1221.