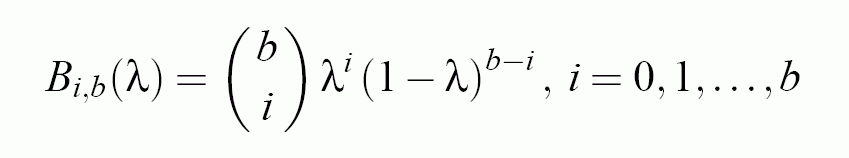
Optimal Cooperative Collision Avoidance between Multiple Robots based on Bernstein-Bezier Curves

Collision avoidance is one of the main issues in applications for a wide variety of tasks in industry, human-supported activities, and
elsewhere. Often, the required tasks cannot be carried out by a single robot, and in such a case multiple robots are used
cooperatively. The use of multiple robots may lead to a collision if they are not properly navigated. Collision-avoidance techniques tend
to be based on speed adaptation, route deviation by one vehicle only, route deviation by both vehicles, or a combined speed and
route adjustment. When searching for the best solution that will prevent a collision many different criteria are considered: time
delay, total travel distance or time, planned arrival time, etc. Our optimality criterion is the minimal total travel distance of
all mobile robots involved in the task, subject to a minimal safety distance between all the robots and subject to velocity and
acceleration constraints of each mobile robot. A short introduction of cooperative collision-avoidance method for multiple nonholonomic
robots with constraints and known start and goal velocities based on Bernstein-B´ezier curves is presented here.

The Bernstein-B´ezier polynomials, which are the base functions in the B´ezier-curve expansion, are given as follows:

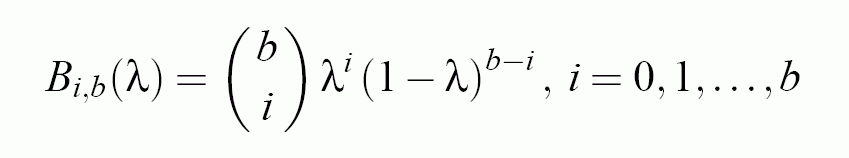
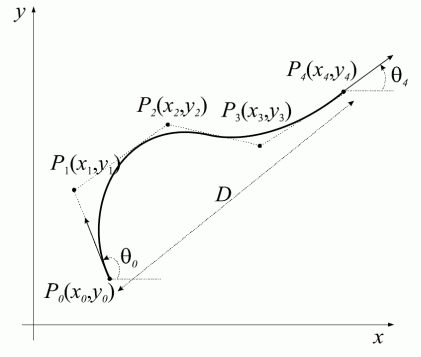
By using five control points P0, P1, P2, P3 and P4 which uniformly define the fourthorder B´ezier curve of 4zh order.

The control point P2 will be defined using optimization, and the control points P1 and P3 are defined from the boundary velocity conditions.

where the vectors to the control points p1 and p3 are defined as follows:

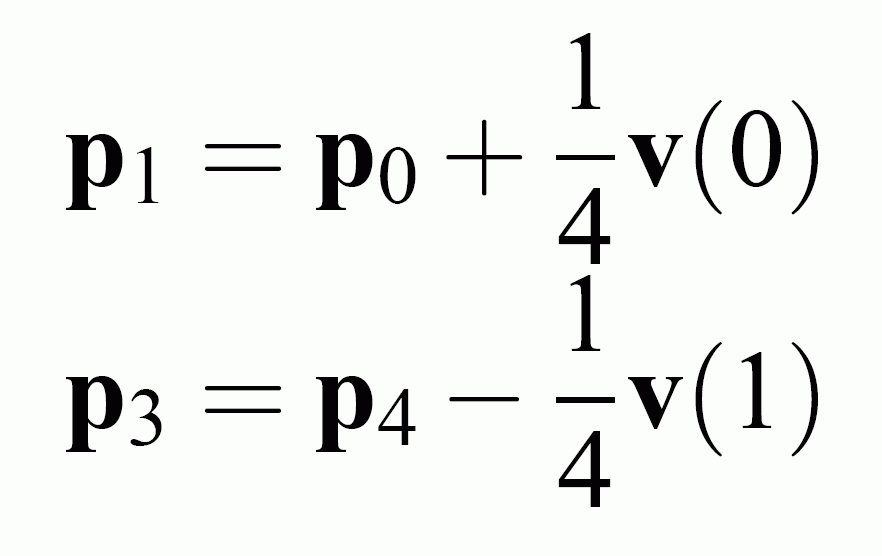
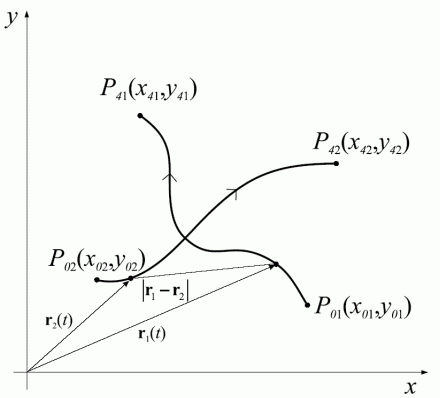
The task of Collision avoidance based on Bernstein-B´ezier curves is to find the shape and velocity profile of the trajectories which will safely drive robots from initial to final positions.

The collision-avoidance problem is now defined as an optimization problem as follows:

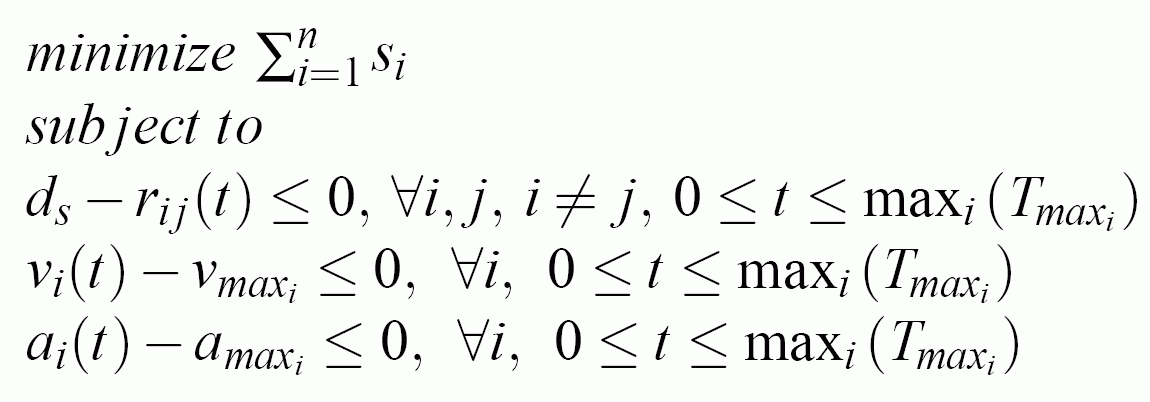
The minimization problem is called an inequality optimization problem. Methods usingpenalty functions transform a constrained problem into an unconstrained problem.

Experimental Results

The path planning results of the optimal cooperative collision avoidance strategy between two and three mobile robots are shown and experimental results obtained on real platform using model predictive trajectory tracking control are given. Experimental set-up.

Experiment with two mobile robots

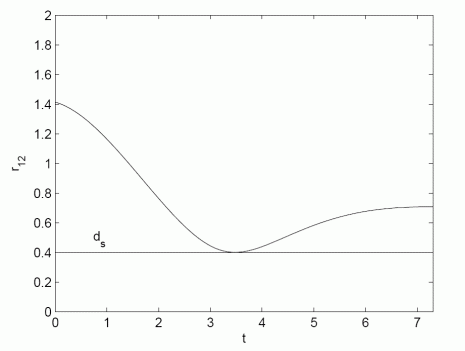
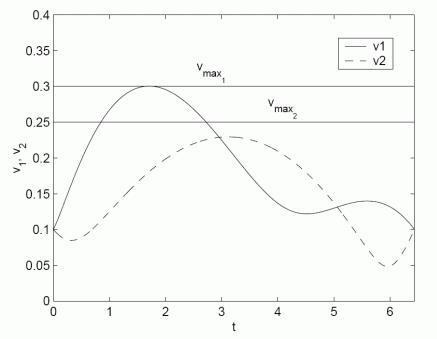
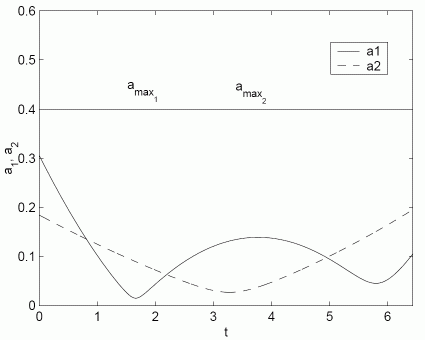
The first figure shows the calculated shapes of trajectories which guaranties collision safe drive of both robots. The second figure shows the distance among robots which is always higher than requested constrained distance ds=0.4 m. The third and the fourth figures shows the velocity and acceleration constraints during experiment. The fifth figure shows real robots experiment where solid line presents robot drive and dashed line  the reference trajectories. The model predictive controller force the robot to follow trajectory despite measurement noise and initial pose errors. And the last figure is the movie of the experiment.

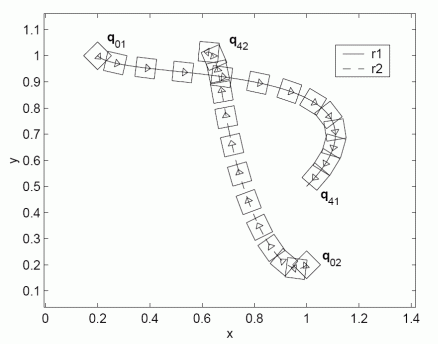
Experiment with three mobile robots

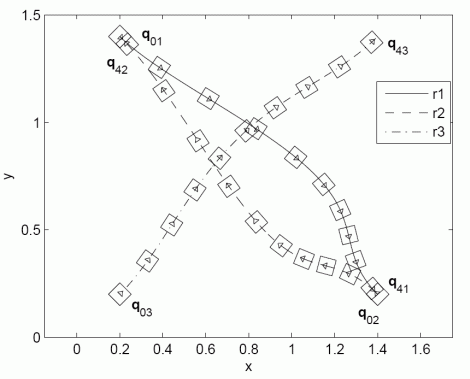
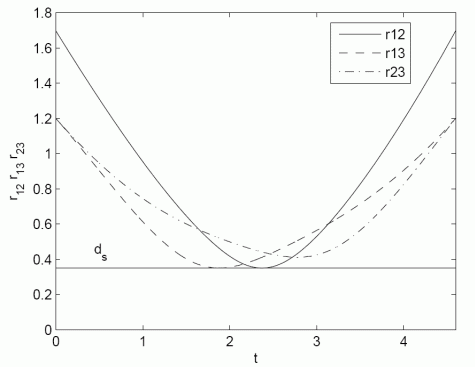
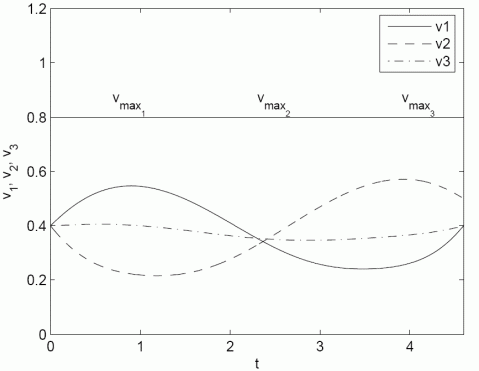
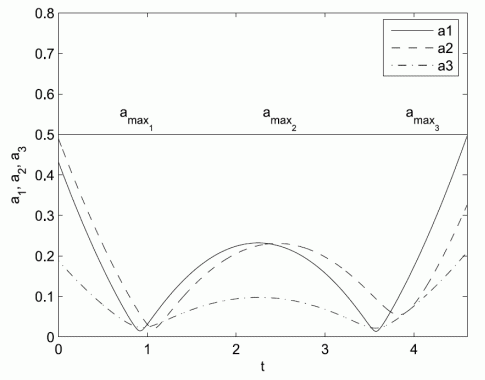
The first figure shows the calculated shapes of trajectories which guaranties collision safe drive of robots. The second figure shows the distance among robots which is always higher than requested constrained distance ds=0.35 m. The third and the fourth figures shows the velocity and acceleration constraints during experiment. The fifth figure shows real robots experiment where solid line presents robot drive and dashed line  the reference trajectories. The model predictive controller force the robot to follow trajectory despite measurement noise and initial pose errors. And the last figure is the movie of the experiment.

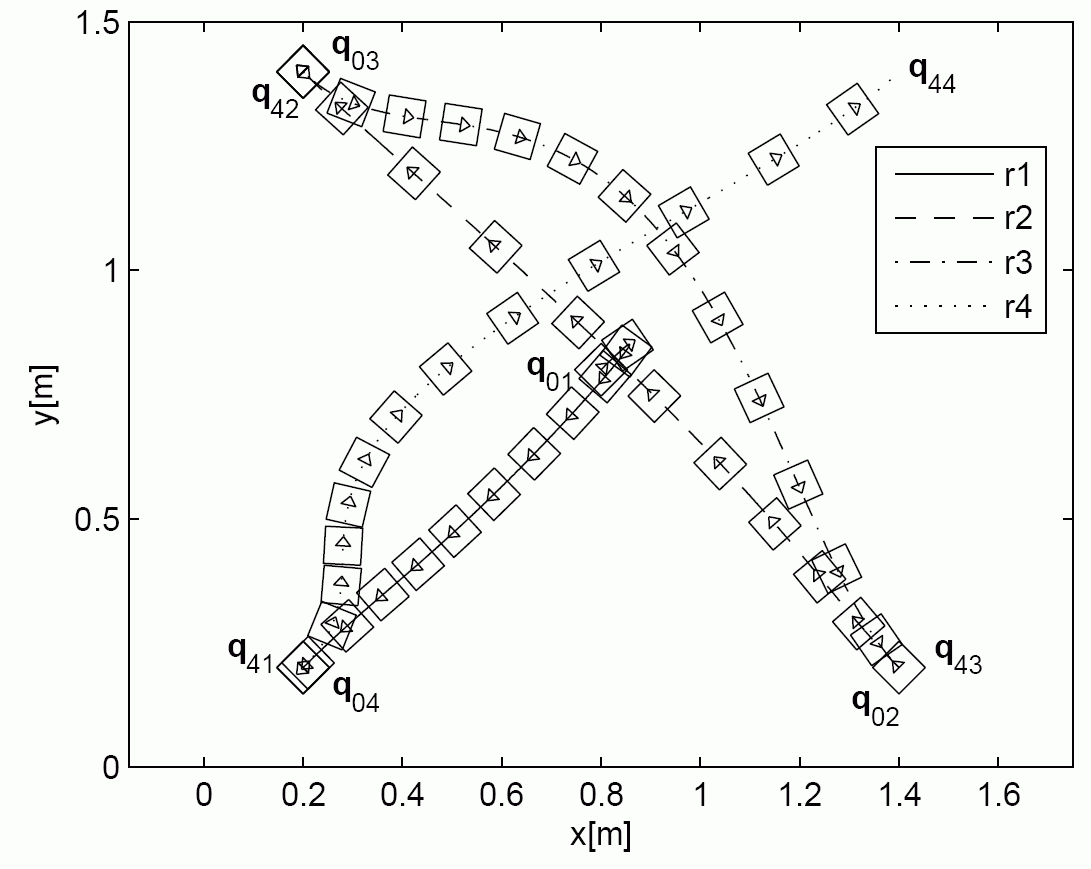
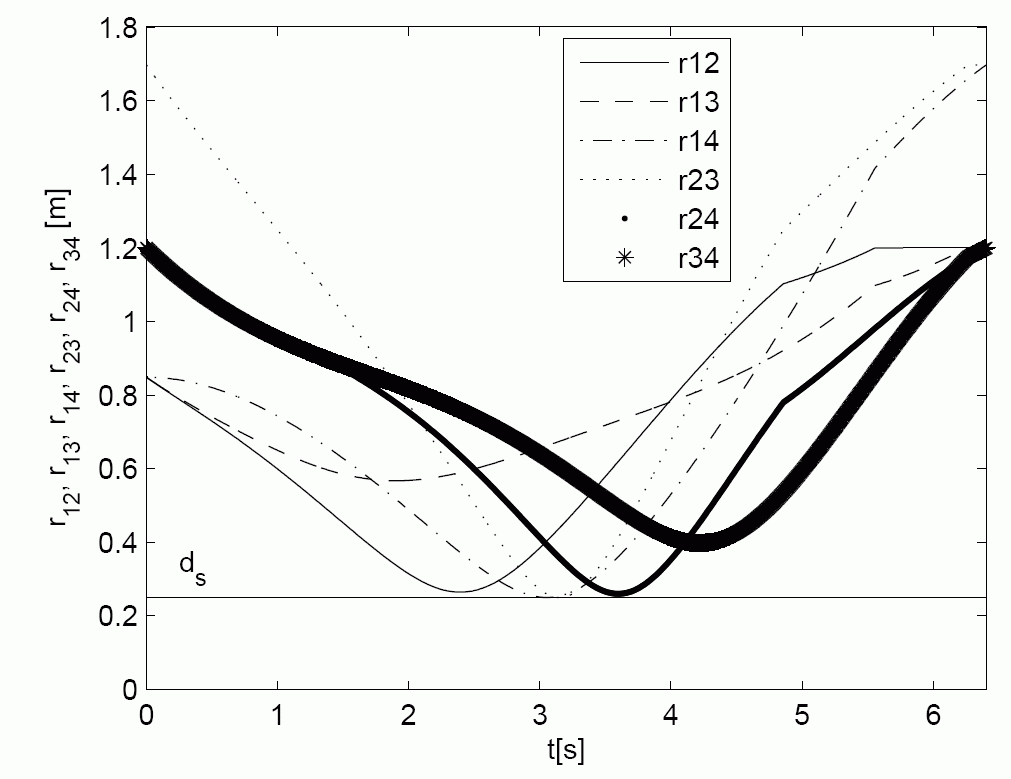
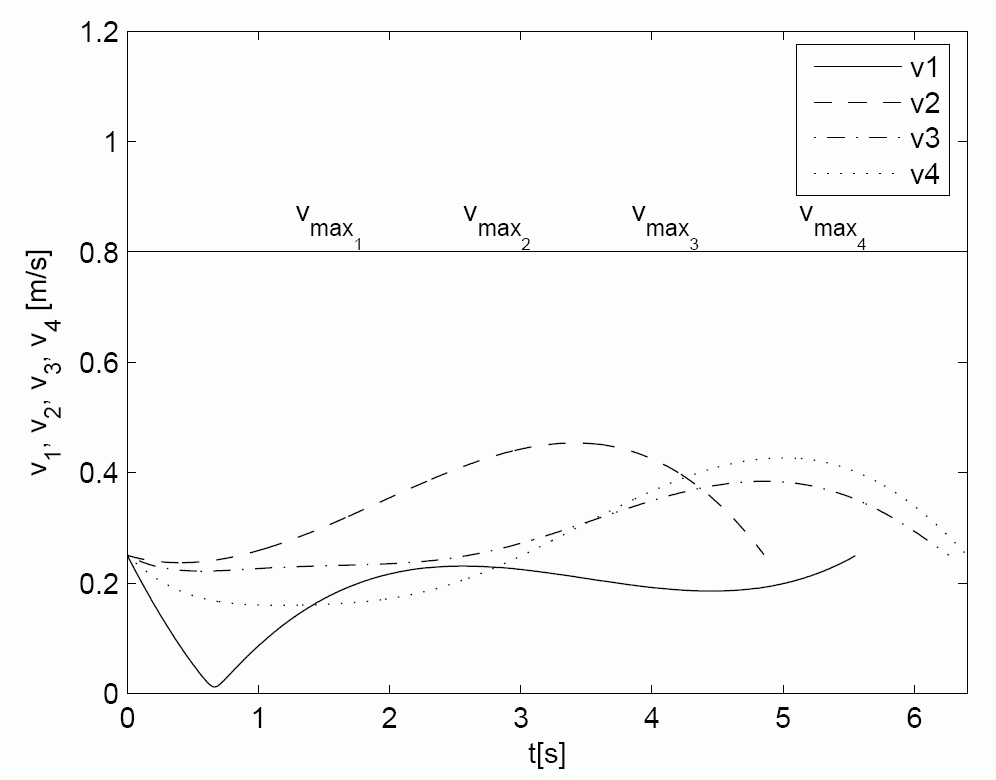
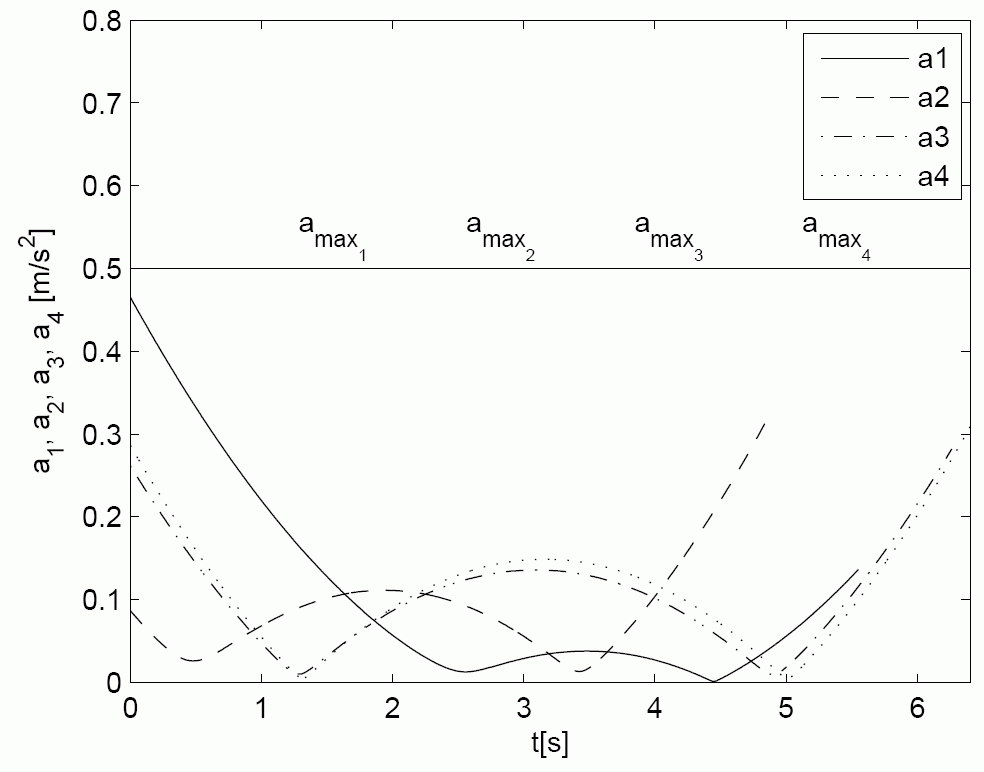
Experiment with four mobile robots

The first figure shows the calculated shapes of trajectories which guaranties collision safe drive of robots. The second figure shows the distance among robots which is always higher than requested constrained distance ds=0.35 m. The third and the fourth figures shows the velocity and acceleration constraints during experiment. The fifth figure shows real robots experiment where solid line presents robot drive and dashed line  the reference trajectories. The model predictive controller force the robot to follow trajectory despite measurement noise and initial pose errors. And the last figure is the movie of the experiment.